Ciencia
Sucesión de Fibonacci, números que te mostrarán la belleza de la naturaleza y del arte
¿Te gustaría descubrir uno de los secretos más fabulosos de la naturaleza? ¿Sabías que existe una secuencia matemática que ha sido la inspiración de los artistas más grandiosos de la historia? La sucesión de Fibonacci tiene todas las respuestas. Sigue leyendo y aprenderás a apreciar de una manera más íntima la naturaleza y el arte.
¿Te gustaría descubrir uno de los secretos más fabulosos de la naturaleza? ¿Sabías que existe una secuencia matemática que ha sido la inspiración de los artistas más grandiosos de la historia? La sucesión de Fibonacci tiene todas las respuestas. Sigue leyendo y aprenderás a apreciar de una manera más íntima la naturaleza y el arte.
Aprende junto a nosotros a como moldear el vidrio
¿Qué es la Sucesión de Fibonacci?
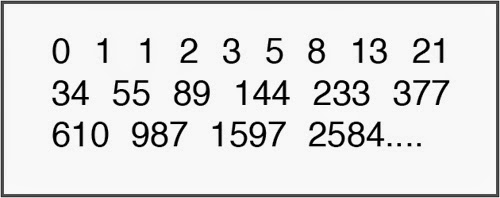
La sucesión de Fibonacci es una serie infinita de números los cuales pueden usarse para describir patrones presentes en la naturaleza. La secuencia comienza por las cifras 0 y 1, para obtener el siguiente número en la sucesión basta con sumar los dos términos que le preceden a este.
Los primeros diez números de la serie son: 0,1,1, 2, 3, 5, 8,13, 21, 34, …
Qué interesante es ver cómo se va creando algo tan grande a través de un inicio simple.
La espiral áurea y su relación con los números de Fibonacci
Usando los números de Fibonacci podremos sacar una forma espiral muy interesante.
Creando cuadrados cuyos lados responden a los números de la serie, se puede dibujar una curva que crece en tamaño tan rápido como la misma sucesión. Esta curva es llamada espiral áurea o espiral dorada.
Las características que cumple dicha figura han sido replicadas en obras de arte a lo largo de la historia. El Partenón de Atenas, construido unos 500 años a.C., fue diseñado respetando las proporciones áureas.
¿Cómo se descubrió la serie de Fibonacci?

En 1202 uno de los matemáticos más importantes de la historia, Leonardo de Pisa, también conocido como Fibonacci, publica su libro Liber Abaci.
Este libro plantea un curioso acertijo:
“Suponiendo que una pareja de conejos cría otra pareja cada mes, y que cada pareja es fértil al cabo de un mes, ¿Cuántos conejos se puede tener al cabo de un año?”
Hagamos una sencilla exposición del problema. Contando las parejas que van naciendo mes tras mes, veremos que la cantidad de parejas coincide con los términos de la serie de Fibonacci.
Analicemos:
Principio del primer mes: Estableceremos que comenzamos con una pareja de conejos recién nacidos, los llamaremos pareja A.
Final del primer mes: Ya la pareja es fértil y está lista para comenzar a reproducirse. 1+0 = 1 parejas en total.
Final del segundo mes: La pareja A dio luz a la pareja B, se vuelve a cruzar la pareja A. 1+1= 2 parejas en total
Final del tercer mes: La pareja A dio nacimiento a la pareja C, ya la pareja B es fértil, se reproducen las parejas A y B. 1+2= 3 parejas en total
Final del cuarto mes: La pareja A parió a la pareja D, y la B a la E, la pareja C ya está lista para reproducirse, 3+2 = 5 parejas en total
En esta tabla te muestro cómo se comporta la serie en el resto de los meses:
| Mes | Cantidad de parejas de conejos a final de mes | Número de la Serie |
| 1ro | 1+0 = 1 pareja en total | 1 |
| 2do | 1+1 = 2 parejas en total | 2 |
| 3ro | 1+2 = 3 parejas en total | 3 |
| 4to | 2+3 = 5 parejas en total | 5 |
| 5to | 3+5 = 8 parejas en total | 8 |
| 6to | 5+8 = 13 parejas en total | 13 |
| 7mo | 8+13 = 21 parejas en total | 21 |
| 8vo | 13+21 = 34 parejas en total | 34 |
| 9no | 21+34 = 55 parejas en total | 55 |
| 10mo | 34+55 = 89 parejas en total | 89 |
| 11no | 55+89 = 144 parejas en total | 144 |
| 12mo | 89+144 = 233 parejas en total | 233 |
Puedes ver claramente cómo se va cumpliendo la serie de Fibonacci en el acertijo. Al final del año, tendremos 233 parejas de conejos, término que ocupa la posición catorce en la serie.
Todos los detalles sobre los corazones artificiales. ¿Cuál es su utilidad?
Ejemplos de la Sucesión de Fibonacci en la naturaleza

Es posible contemplar lo hermoso de la naturaleza, lo perfecta que es, observando los patrones que sigue la sucesión de Fibonacci en ella.
Un gran ejemplo de esto lo encontramos en la botánica. Las ramas y las hojas de las plantas se distribuyen buscando siempre recibir el máximo de luz para cada una de ellas. Por eso ninguna hoja nace justo en la vertical de la anterior. La distribución de las hojas alrededor del tallo se produce siguiendo secuencias basadas exclusivamente en los números de esta serie.
- El número de espirales en múltiples flores y frutos se ajustan a parejas consecutivas de términos de la sucesión. Los girasoles tienen 55 en un sentido y 89 en el otro. Los más grandes tienen 89 y 144.
- Las margaritas presentan las semillas en forma de 21 y 34 espirales.
- Las piñas de cualquier variedad tienen siempre una cantidad de roscas que coinciden con dos números consecutivos de la Sucesión de Fibonacci, 5 y 8, o bien, 8 y 13.
- La forma de algunas especies de caracol, como el Nautilus, cumplen perfectamente con las dimensiones de la espiral áurea.
- Podemos establecer relación directa entre la serie de Fibonacci y el árbol genealógico de cada abeja, similar al ejemplo usado en Sucesión de Fibonacci conejos, el acertijo.
Parece que el mundo vegetal tiene programado en su genética los números de Fibonacci. Este matemático, sin pretenderlo, descubrió la clave del crecimiento de la naturaleza.
Esta es la verdad que se oculta tras la cámara de tu teléfono
Ejemplos de la Serie de Fibonacci en el arte
Muchos pintores, arquitectos, músicos, buscando proporciones estéticas en sus obras han terminado replicando la Sucesión de Fibonacci, ya sea de manera accidental o de manera intencional.
- El artista italiano Mario Merz, perteneciente al movimiento Arte Povera, basó gran parte de su obra en la progresión de Fibonacci. Desarrolló muchas esculturas con cierta filosofía: “cada número resulta de la suma de los dos precedentes”.
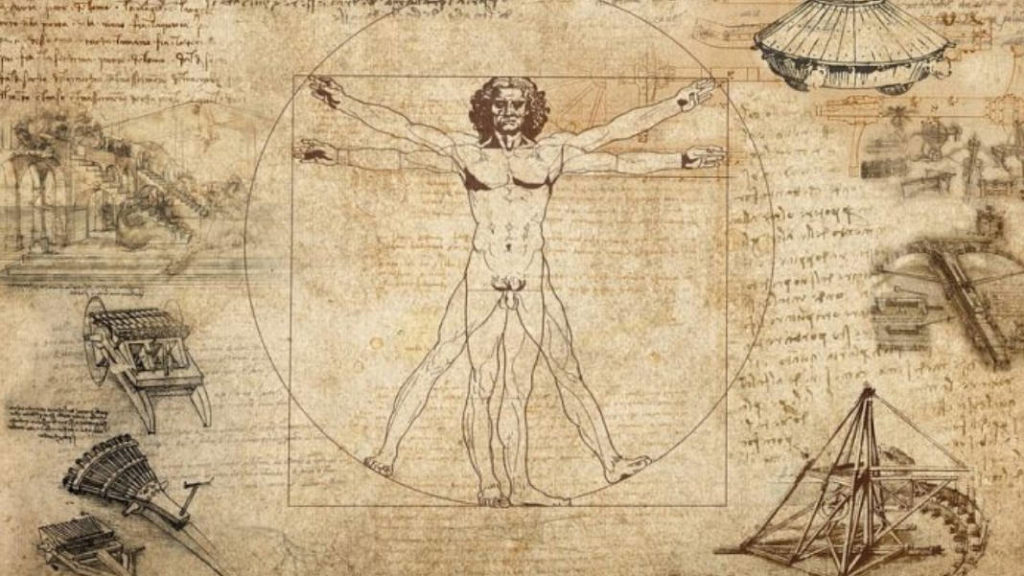
- “Hombre de Vitruvio”, dibujo acompañado por estudios anatómicos realizados por el célebre Leonardo Da Vinci, es otro ejemplo. Plasma como las proporciones del cuerpo humano siguen la serie de Fibonacci. Las establece como fracciones de estos números.
- Una de las obras maestras creadas por el pintor Pablo Picasso, “Guernica”, puede subdividirse geométricamente en varios cuadrados áureos.
- Los pentagramas formales de las sonatas que regaló al mundo el compositor Wolfgang Amadeus Mozart presentan arreglos inspirados en dicha sucesión.
- Los elementos de uno de los cuadros elaborados por el pintor surrealista español Salvador Dalí siguen proporciones áureas. Se trata de “Media taza gigante volante con anexo inexplicable de cinco metros de longitud”.

-

 Salud5 años ago
Salud5 años agoBorra las manchas en las manos cariño
-
 Curiosidades4 años ago
Curiosidades4 años agoCientífico holandés revela por qué los mosquitos solo pican a algunas personas… ¿serás tú la próxima víctima?
-

 Curiosidades2 años ago
Curiosidades2 años agoHermosos vestidos de pasarela que las celebridades lucieron en la alfombra roja
-

 Consejos3 años ago
Consejos3 años ago¿Cómo eliminar las manchas en mi piel? El remedio que en solo 2 noches te sana
-

 Curiosidades2 años ago
Curiosidades2 años ago10 señales: ¿Cómo saber si tu pareja te quiere dejar?
-

 Curiosidades4 años ago
Curiosidades4 años agoAnciana arrestada cumple el mayor deseo de su vida.
-

 Curiosidades3 años ago
Curiosidades3 años agoPocos saben esto del orégano
-

 Salud4 años ago
Salud4 años agoDescubre el por qué del ardor al orinar










You must be logged in to post a comment Login